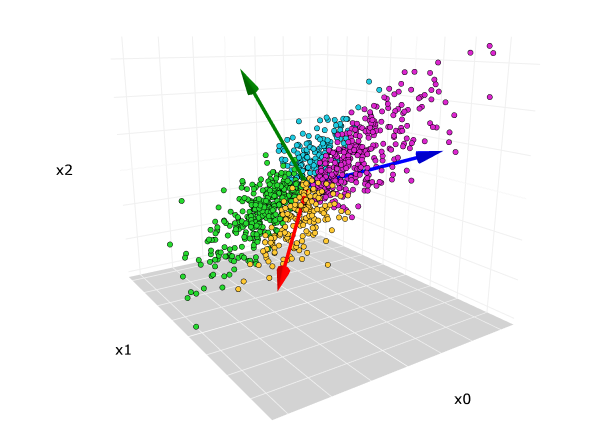
Dimension reduction with Principal Component Analysis

There are different technique to reduce dimensionality. One of the most known is Principal Component Analysis (PCA). Probably the most known one. The aim of this article is to explain the math behind PCA. It is based on eigen decomposition.

PCA is based on the properties of symmetric matrices and eigen decomposition.
Let’s consider the set of vectors { \( x_1,…,x_n \) } that represent our data.

How to apply PCA

Step 1 : Compute the mean and substract it to get data with null Esperance

$$x_i=x_i-\frac{1}{n} \sum_{i=1}^n x_i$$

Step 2 : Compute the covariance matrix

$$C = \frac{1}{n} \sum _{i=1}^n x_ix_i^T$$

Step 3 : Eigen decomposition

For a matrix M, an eigen value \( \lambda \) with the associated eigen vector \( u \) verify \( Mu = \lambda u \).

The covariance matrix \(C\) is symmetric, so we can apply the eigen decomposition \(C = \sum_{i=1}^n \lambda_i u_i u_i^T \) with \( \lambda_1 \geq \lambda_2 \geq …. \geq \lambda_n \)

Step 4 : Projection onto eigenvectors

Let’s consider that we want to reduce the dimension from n to m. We just need to project the data onto the m first eigen vectors because they have the highest eigen values. We then get the result: $$ \forall i \in { 1,…,n } , x_i' = [u_1^Tx_i,….,u_m^Tx_i]^T$$

Generalisation to any kernel : Kernel PCA

Let’s consider a kernel with the expression \( k(x,y)= \phi(x) \phi(y)^T \). For instance a gaussian kernel can be written as \( k(x,y)= \frac{1}{\sqrt{2 \pi }\sigma} e^{- \frac{ {||x-y|| }^2}{2 \sigma^2} } \)
We can define \( \phi_i:=\phi(x_i) \) and consider the matrix \( C = \sum_{i=1}^n \phi_i \phi_i ^T \)

You may be able to better understand the PCA now. Do not hesitate if you have any questions.