RALD-LARD Machine
A model of computation is a theoretical framework that abstracts the essential features of a computing system, allowing us to analyze and compare different algorithms and machines based on their computational power and efficiency. In computer science, models of computation are used to study the limits and possibilities of computation, and to explore the relationships between different computational problems and their solutions. By formalizing the notion of computation, models of computation have become essential tools for theoretical computer scientists, algorithm designers, and anyone interested in understanding the nature and scope of computation.
This blog post introduces a new model of computation inspired from cyclic tag system and unary numeral system.
1- RALD-LARD Machine : A new model of computation
1.1- Definition
Rigorously, a RALD-LARD machine is a 4-tuple $(N,O,C,I)$ where:
- $N$ is a positive integer representing the number of inputs that the machine can accept. These inputs are expected to be in string format.
- $O$ is the delimiter, which is present only once in each input of the machine.
- $C$ is the repeated character, which can be present in all the inputs of the machine.
- $I$ is a set of instructions, which are performed in a loop by the machine for a given set of inputs.
1.2- Input and output modalities
As described above the inputs of a RALD-LARD machine $(N,O,C,I)$ are strings with the following format :
$$X = { {CC \cdots CC} _{n \geq 0} O {CC \cdots CC} _{m \geq 0} }$$
Given $n \in \mathbb{N}$, its representation as an input to a RALD-LARD machine can be $ {CC \cdot \cdot \cdot CC} _{n\geq0}O$ or $O {CC \cdot \cdot \cdot CC} _n \geq 0$. The first can be referred to as the left representation, while the latter can be referred to as the right representation. For example, the right representation of $3$ is $OCCC$ and the left representation of $4$ is $CCCCO$.
The outputs have the same format as the inputs. If an output is in the left or the right representation it is then referred to as a meaningful output because it can represent a number.
1.3- Principle
A RALD-LARD machine $(N,O,C,I)$ operates on the following principle:
- The set of instructions are executed in a loop to modify the inputs until the machine stops.
- Each instruction performs an action in a given direction for a specific input.
- There are two actions: Add and Delete.
- There are two directions: Left and Right.
- An input in an instruction can be represented by a unique identifier.
- Each instruction adds or deletes the repeated character $C$ to the right or to the left of the delimiter $O$ for a specific input.
- If deletion is impossible, meaning that there are no $C$ in the specified direction (left, right), the machine will stop.
A set of instructions $I$ can be represented by a table of size $p\times3$, where $p$ is the number of instructions in the set: $$ \begin{pmatrix} action_1 & direction_1 & id_1 \\ \vdots & \vdots & \vdots \\ action_p & direction_p & id_p \end{pmatrix} $$ When there is only one input the machine is called mono RALD-LARD machine and the inputs ids can be omitted from the set. In that case a set of instructions can be represented by a table of size $p\times2$ :
$$ \begin{pmatrix} action_1 & direction_1 \\ \vdots & \vdots \\ action_p & direction_p \end{pmatrix} $$
Let consider a machine with a set of instructions $I = \begin{pmatrix} D & R & 1 \\ A & L & 1 \\ D & R & 2 \\ A & R & 1 \end{pmatrix}$. This machine takes 2 inputs and the instructions are performed in a loop from top to bottom. The table below summarizes the steps performed for the inputs $OC$ and $OC$:
| Step | Instruction | Input 1 | Input 2 |
|---|---|---|---|
| inputs | $$OC$$ | $$OC$$ | |
| 1 | $$D \, L \, 1$$ | $$OC$$ | $$OC$$ |
| 2 | $$A \, L \, 1$$ | $$COC$$ | $$OC$$ |
| 3 | $$D \, R \, 2$$ | $$COC$$ | $$O$$ |
| 4 | $$A \, R \, 1$$ | $$COCC$$ | $$O$$ |
| 5 | $$D \, R \, 1$$ | $$COC$$ | $$O$$ |
| 6 | $$A \, L \, 1$$ | $$CCOC$$ | $$O$$ |
| 7 | $$D \, R \, 2$$ | $$CCOC$$ | HALT |
| outputs | $$CCOC$$ | $$O$$ |
The machine will always halt if, for at least one of the inputs, there are more deletions than appendings in the set of instructions.
1.4- Mathematical representation
A RALD-LARD machine can be represented as a function from the set of inputs to the set of outputs. Let consider a machine $(N,O,C,I)$, $X = { {CC \cdots CC} _{n \geq 0} O {CC \cdots CC} _{m \geq 0} }$ and $q \in \mathbb{N}$. The function $f$ representing the machine can be defined as :
$$\begin{align} f\colon X^q \rightarrow X^q \\ x\mapsto I \xrightarrow{\text{loop}} x \end{align} $$
In most cases, the machine takes inputs in either the left or the right representation. Therefore, we can consider subsets of $X$ such as $X_l ={ {CC \cdots CC} _{n \geq 0} O }$ for the left representation and $X_r = O {CC \cdots CC} _{m \geq 0}$ for the right representation.
2- Computational processes
The machine as defined previously can perform a variety of arithmetic computations. Here are some examples :
| Computation process | Domain and Codomain | Set of Instructions | Steps |
|---|---|---|---|
| $n+1, n \in \mathbb{N}$ | $X_r \rightarrow X_r$ | $I = \begin{pmatrix} A & R \\ D & L \end{pmatrix}$ | $1$ |
| $n-1, n \in \mathbb{N}$ | $X_r \rightarrow X_r$ | $I = \begin{pmatrix} D & R \\ D & L \end{pmatrix}$ | $1$ |
| $\left\lfloor \frac{n}{2} \right\rfloor, n \in \mathbb{N}$ | $X_r \rightarrow X_l$ | $I = \begin{pmatrix} D & R \\ D & R \\ A & L \end{pmatrix}$ | $\left\lfloor \frac{3n}{2} \right\rfloor$ |
| $\left\lfloor \frac{n}{m} \right\rfloor, n \in \mathbb{N}, m \in \mathbb{N}^*$ | $X_r \rightarrow X_l$ | $I = \begin{pmatrix} D & R \\ \vdots & \vdots \\ D & R & \\ A & L \end{pmatrix}$,$[m+1,2]$ | $\left\lfloor \frac{(m+1)n}{m} \right\rfloor$ |
| $2n, n \in \mathbb{N}$ | $X_r \rightarrow X_l$ | $I = \begin{pmatrix} D & R \\ A & L \\ A & L \end{pmatrix}$ | $3n$ |
| $n \times m, n \in \mathbb{N}, m \in \mathbb{N}^*$ | $X_r \rightarrow X_l$ | $I = \begin{pmatrix} D & R \\ A & L \\ \vdots \\ A & L \end{pmatrix}$, $[m+1,2]$ | $(m+1)n$ |
| $\text{Parity of } n, n \in \mathbb{N}$ | $X_r \rightarrow X_l$ | $I = \begin{pmatrix} D & R \\ A & L \\ D & R \\ D & L \end{pmatrix}$ | $2n$ |
| $n + m, n \in \mathbb{N}, m \in \mathbb{N}$ | $X_r^2 \rightarrow X_r^2$ | $I = \begin{pmatrix} D & R & 2 \\ A & R & 1 \end{pmatrix}$ | $2m$ |
| $n - m, n \in \mathbb{N}, m \in \mathbb{N}$ | $X_r^2 \rightarrow X_r^2$ | $I = \begin{pmatrix} D & R & 2 \\ D & R & 1 \end{pmatrix}$ | $2\min{(n,m)}$ |
| $\text{Compare } n \text{ to } m, n \in \mathbb{N}, m \in \mathbb{N}$ | $X_r^2 \rightarrow X^2$ | $I = \begin{pmatrix} D & R & 1 \\ A & L & 1 \\ D & R & 2 \\ D & L & 1 \end{pmatrix}$ | $\leq 4\min{(n,m)}$ |
Most of the computations in this table are available on the RALD-LARD GitHub page.
3- Limitations of RALD-LARD machines
The stateless machine exhibits proficiency in basic arithmetic computations. However, it is unable to perform recursion-based computations, such as the multiplication of two inputs (m x n) without a lengthy set of instructions. The model lacks the ability to reuse inputs multiple times due to the halting definition, which significantly impacts its efficiency in solving complex problems.
Non-arithmetic problem solving presents a challenge for the machine, as its architecture primarily focus on arithmetic tasks, limiting its ability. The absence of states in the model hinders its capacity to solve state-based problems that rely on the representation and manipulation of information over time.
4- Stacked RALD-LARD machine
The idea of having a machine unable to perform recursion is a huge problem in itself. To solve this issue stacked RALD-LARD machines are introduced, inspired by graph theory and the idea of stacking models.
A stacked RALD-LARD machine is a quadruplet $(M,E,I,\phi)$ where:
- $M$ is a set of RALD-LARD machines that includes a machine $M_0$ as the starting point.
- $E \subseteq { (P,Q) , | , (P,Q) \in M^2 }$, a set of directed arcs
- $\phi : E \rightarrow I$, a transition function with I being a set of instructions called transition instructions
- The transition instructions are executed on the outputs of a RALD-LARD machine before they become the inputs of the next RALD-LARD machine
A stacked RALD-LARD machine can then be considered as a model gathering multiple RALD-LARD machines passing the inputs from one machine to another as long as the transition instructions ($\phi$) do not fail. A stacked RALD-LARD machine halts only and only if one of the transition instructions cannot be performed.
Computation of $2^n$
The computation of $2^n$ is computed with the stacked machine below taking as inputs the right representation of $n = O{ {CC \cdot \cdot \cdot CC }}_{n\geq0}$ and the right representation of $1 = OC$:
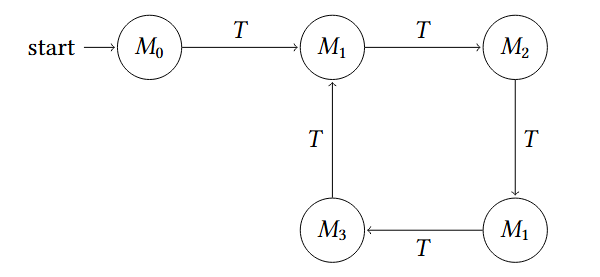
$T = \begin{pmatrix} D & R & 0\\ D & L & 0 \end{pmatrix}$, $M_0 \equiv \begin{pmatrix} A & R & 0\\ D & L & 0 \end{pmatrix}$, $M_1 \equiv \begin{pmatrix} D & R & 0\\ D & L & 0 \end{pmatrix}$, $M_2 \equiv \begin{pmatrix} D & R & 1\\ A & L & 1\\ A & L & 1 \end{pmatrix}$, $M_3 \equiv \begin{pmatrix} D & L & 1\\ A & R & 1\\ A & R & 1 \end{pmatrix}$
$M_0$ computes $n+1$ for $n$ in the right representation, $M_1$ computes $n-1$ for $n$ in the right representation, $M_2$ computes $2n$ for $n$ in the right representation and $M_3$ computes $2n$ for $n$ in the left representation.
Conclusion
Overall, models of computation provide a framework for analyzing and comparing computing systems. The RALD-LARD machine introduced here excels in basic arithmetic computations but struggles with recursion and non-arithmetic problems. To address these limitations, stacked RALD-LARD machines are proposed, inspired by graph theory and model stacking. These advancements aim to enhance computational power and address state-based scenarios.
References
Introduction to Automata Theory, Languages, and Computation